Dijkstra's algorithm

Introduction

To find the shortest path between a picked node and all other nodes in a weighted graph. Starting from a specified node, it calculates the distances between itself and all other nodes in a graph.

How it works:

1. Starting at 1 (A), calculate distances. This is known as the source.

   distances = {"1": 0, "2": 7, "3": 9, "4": inf, "5": inf, "6": 14}
   unvisited_nodes = {"2", "3", "4", "5", "6"}
   visited_nodes = ["1"]

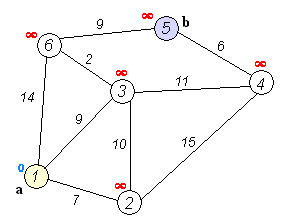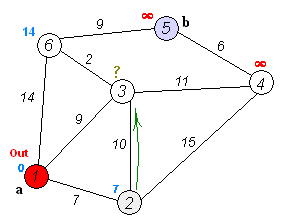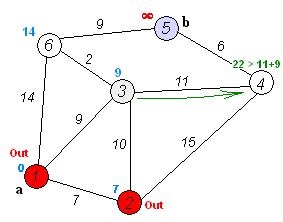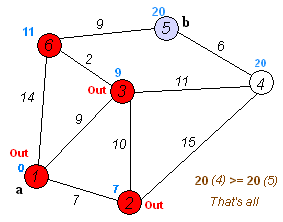
2. Travel to the next unvisited node with the shortest distance from the source. In the first iteration, it will be node 2, as it has the distance of 7.

3. Calculate the distance for each unvisited node of the current node (cost of path to current node + to unvisited neighbour). If the calculated distance is less than the pre-existing value, update distances.

# First iteration
distances = {"1":0, "2": 7, "3": 9, "4": 22, "5": inf, "6": 14}
visited_nodes = ["1", "2"]
# 3 and 4 is reachable from the current node of 2. However, it costs more to travel to 3 from 2 (7+10 > 9), so the pre-existing distance of 9 will be kept. 4 is now reachable with the cost of 7 + 15 = 22 which is < inf, so it will be updated.

4. Go back to step 2, starting the next iteration.

# Second iteration
current_node = "3" # 3 is the next node with shortest distance of 9
distances = {"1":0, "2": 7, "3": 9, "4": 20, "5": inf, "6": 9+2}
visited_nodes = ["1", "2", "3"]
 
# Third iteration
current_node = "6" # 6 is the next node with shortest distance of 11
distances = {"1":0, "2": 7, "3": 9, "4": 20, "5": 11+9, "6": 11}
visited_nodes = ["1", "2", "3", "6"]
 
# Fourth iteration
current_node = "4" # 4 is the next node with the shortest distance of 20
distances = {"1":0, "2": 7, "3": 9, "4": 20, "5": 20, "6": 11} # no updates
visited_nodes = ["1", "2", "3", "6", "4"]
 
# Fifth iteration - because there are no more unvisited nodes, there isn't a 5th iteration.
 
return distances # therefore, the distances from A to all other nodes are defined in distances.

Sample code

I personally wrote this, so it’s definitely not the best way of doing Dijkstra’s, but it’s definitely a method.

# Define a matrix to represent distances between nodes
 
matrix = {
    "A": {"A": 0, "B": 7, "C": 9, "D": None, "E": None, "F": 14},
    "B": {"A": 7, "B": 0, "C": 10, "D": 15, "E": None, "F": None},
    "C": {"A": 9, "B": 10, "C": 0, "D": 11, "E": None, "F": 2},
    "D": {"A": None, "B": 15, "C": 11, "D": 0, "E": 6, "F": None},
    "E": {"A": None, "B": None, "C": None, "D": 6, "E": 0, "F": 9},
    "F": {"A": 14, "B": None, "C": 2, "D": None, "E": 9, "F": 0}
}
 
 
def dijkstra(matrix, source):
    # Get the distances from the source node to all other nodes
    start_vertex = matrix[source]
    print(start_vertex)
    
    # Initialize distances from the source to all nodes
    # If there is no direct path, set the distance to infinity
    distances = {node: start_vertex[node] if start_vertex[node] is not None else float('inf') for node in matrix}
    
    # List to keep track of visited nodes
    visited_nodes = [source]
 
  
    # Variable to keep track of the number of iterations
    iteration = 0
 
 
    # Loop until all nodes have been visited
    while len(visited_nodes) < len(matrix):
        print("\n")
        iteration += 1
        print("Iteration: ", iteration)
        print("Visited nodes: ", visited_nodes)
        print("Distances: ", distances)
  
 
        # Initialize the minimum distance to infinity
        min_distance = float("inf")
        min_vertex = None
 
 
        # Get the list of potential nodes to visit next
        potential_nodes = [node for node in distances if distances[node] != None and node not in visited_nodes]
        print("potential nodes:", potential_nodes)
 
        # Find the node with the smallest distance
        for node in range(len(potential_nodes)):
            if distances[potential_nodes[node]] < min_distance:
                min_distance = distances[potential_nodes[node]]
                min_vertex = potential_nodes[node]
        print("min_vertex: ", min_vertex)
 
        visited_nodes.append(min_vertex) # add minimum vertex to visited nodes
 
        neighbours = [node for node in matrix[min_vertex] if matrix[min_vertex][node] != None and node not in visited_nodes] # check neighbours of miminum vertex
 
        print("neighbours: ", neighbours)
        for node in neighbours:
            print("node:", node, matrix[min_vertex][node])
            # if current distance is larger than new path, then update it. 
            if distances[node] > distances[min_vertex] + matrix[min_vertex][node]:
                distances[node] = distances[min_vertex] + matrix[min_vertex][node]
    return distances
 
print(dijkstra(matrix, "A"))

Transclude of dijkstra.py